1343. Maximum Product of Splitted Binary Tree

https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/

Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

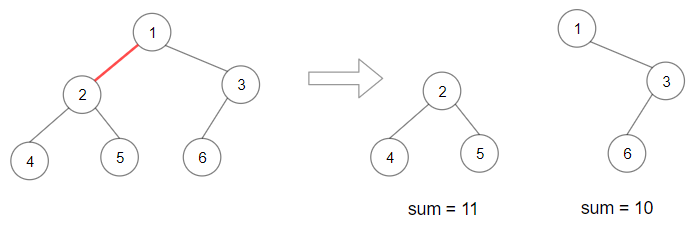
Input: root = [1,2,3,4,5,6]
Output: 110
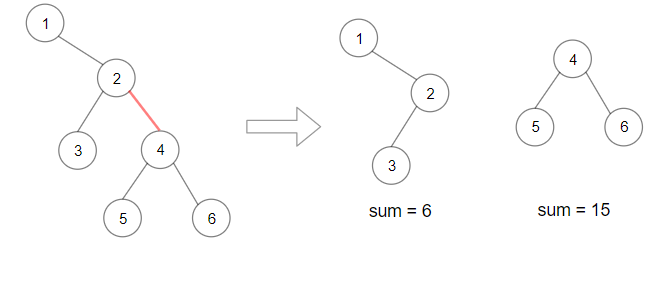
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation:  Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

二叉树一条边能把树分成两棵，问能任意去掉一条边，两棵树各自的和相乘最大会是多少。遍历统计出整棵树的和，再遍历每个结点统计出该结点的子树和是多少，再看当前子树的和 * (sum - 当前子树和)是否是最大解。也可以用集合统计出所有可能的和，再分别看它们所形成的乘积最大是多少。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    const unsigned int M = 1000000007;
    long res = 0;
    int sum(TreeNode *node, long total = 0) {
        if (node == nullptr) return 0;
        int l = sum(node->left, total);
        int r = sum(node->right, total);
        const int s = l + r + node->val;
        res = max(res, s * (total - s));
        return s;
    }
    
    int maxProduct(TreeNode* root) {
        const int total = sum(root);
        sum(root, total);
        return res % M;
    }
};