1457. Pseudo-Palindromic Paths in a Binary Tree

https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

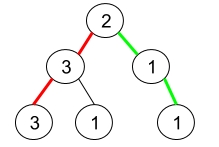
Example 2:

Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

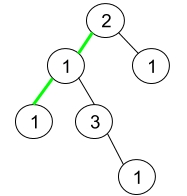
Example 3:

Input: root = [9]
Output: 1

Constraints:

• The given binary tree will have between 1 and 10^5 nodes.

• Node values are digits from 1 to 9.

二叉树的结点值为[0~9]，统计能通过permutation变成回文的(从root到叶的)路径数。能通过permutation成为回文需要满足至多有一个元素出现奇数次。由于值的范围是0到9，因此可以利用一个整数cnt和位操作统计出现频率，位的位置代表对应的值频率，当为1时是奇数，偶数时是0，并在对应位做异或。当只有一个1时，cnt和cnt-1相与为0。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
            
    def pseudoPalindromicPaths (self, root: TreeNode) -> int:
        def dfs(node, cnt):
            if not node: return 0
            cnt ^= 1 << node.val
            res = dfs(node.left, cnt) + dfs(node.right, cnt)
            if node.left == node.right:
                if cnt & (cnt - 1) == 0:
                    res += 1
            return res
        return dfs(root, 0)