1444. Number of Ways of Cutting a Pizza

https://leetcode.com/problems/number-of-ways-of-cutting-a-pizza/

Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts.

For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.

Return the number of ways of cutting the pizza such that each piece contains at least one apple. Since the answer can be a huge number, return this modulo 10^9 + 7.

Example 1:

Input: pizza = ["A..","AAA","..."], k = 3
Output: 3 
Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.

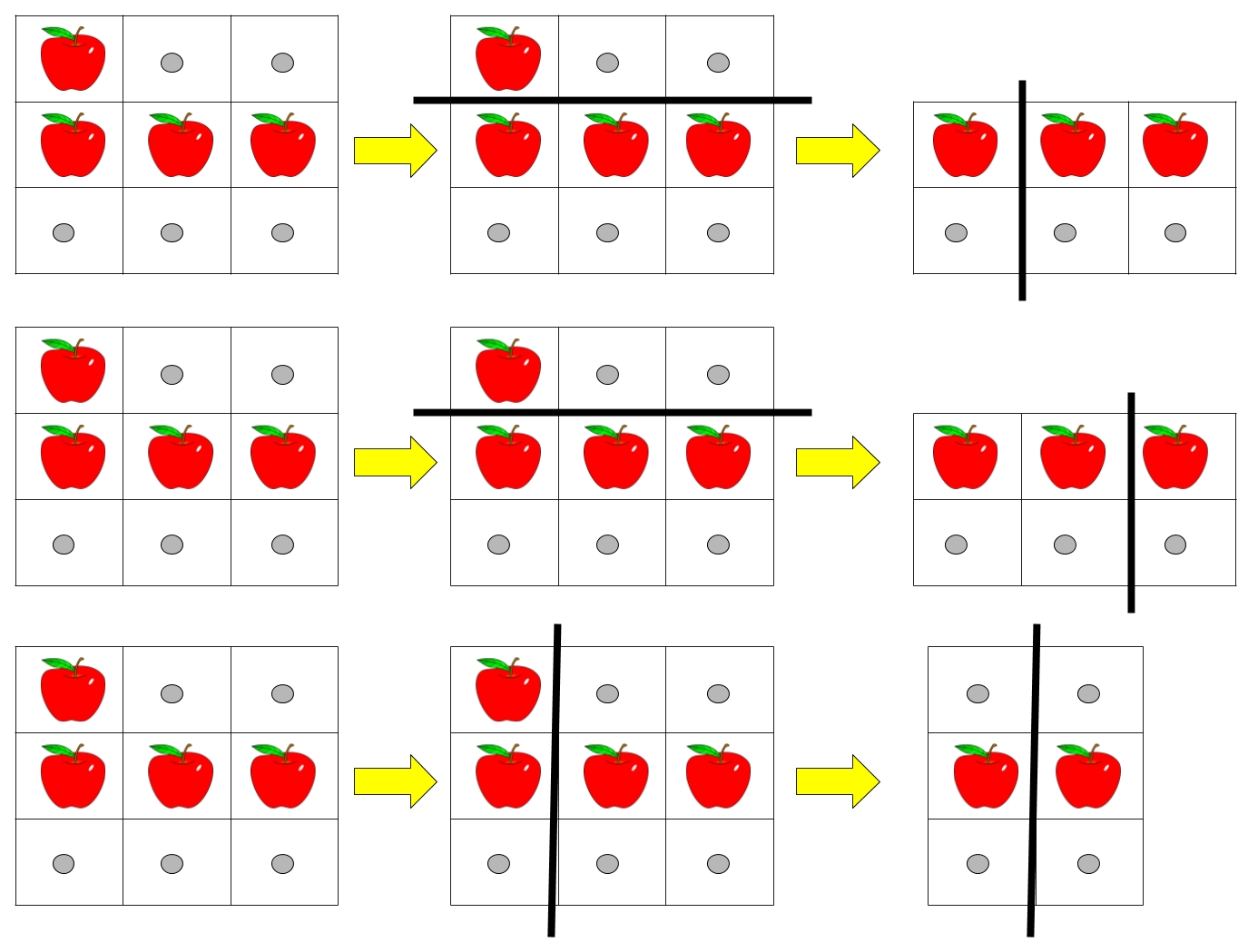
Example 2:

Input: pizza = ["A..","AA.","..."], k = 3
Output: 1

Example 3:

Input: pizza = ["A..","A..","..."], k = 1
Output: 1

Constraints:

• 1 <= rows, cols <= 50

• rows == pizza.length

• cols == pizza[i].length

• 1 <= k <= 10

• pizza consists of characters 'A' and '.' only.

方格上有苹果，每次能沿着行或列切割，并把上面或左边的苹果分出去，要求每次都能分出至少一个苹果，问一共有多少种分法。找所有的情况=> DP/DFS。从（0,0）起点开始，遍历所有可能的切割方式，检查切割后上或左侧是否有苹果。如有，切割后的剩下的格子是独立子问题，因此可以用DFS + memo记忆化递归该子问题。判断指定范围内格子是否有苹果 => Range Sum Immutable 2D。

思路参考自花花

class Solution:
    def ways(self, pizza: List[str], K: int) -> int:
        M, N, MOD = len(pizza), len(pizza[0]), 10 ** 9 + 7
        apple = [[0] * (N + 1) for _ in range(M + 1)]
        memo = [[[-1] * K for _ in range(N)] for _ in range(M)]
        for j in range(N):
            for i in range(M):
                apple[i + 1][j + 1] = apple[i + 1][j] + apple[i][j + 1] - apple[i][j]
                apple[i + 1][j + 1] += 1 if pizza[i][j] == 'A' else 0
        def has(r1, c1, r2, c2):
            return (apple[r2 + 1][c2 + 1] - apple[r1][c2 + 1] - apple[r2 + 1][c1] + apple[r1][c1]) > 0
        def dfs(r, c, k):
            if memo[r][c][k] != -1:
                return memo[r][c][k]
            if k == 0:
                return 1 if has(r, c, M - 1, N - 1) else 0
            res = 0
            for i in range(r, M - 1):
                if has(r, c, i, N - 1):
                    res = (res + dfs(i + 1, c, k - 1)) % MOD
            for j in range(c, N - 1):
                if has(r, c, M - 1, j):
                    res = (res + dfs(r, j + 1, k - 1)) % MOD
            memo[r][c][k] = res
            return res
        return dfs(0, 0, K - 1)