1631. Path With Minimum Effort

https://leetcode.com/problems/path-with-minimum-effort/

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

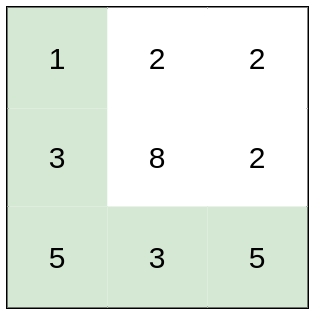
Example 2:

Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

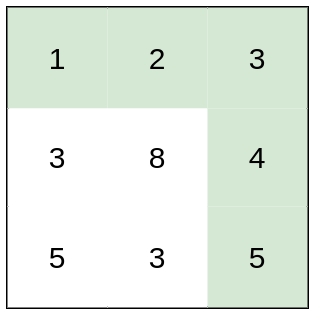
Example 3:

Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

• rows == heights.length

• columns == heights[i].length

• 1 <= rows, columns <= 100

• 1 <= heights[i][j] <= 106

整数构成的矩阵中找从左上角到右下角所有路线中找满足其中任意相邻俩格子绝对差最小的，返回该绝对值。直观做法是DFS + memo，超时。进一步可以把矩阵看成图，元素作为点，点点之间边的权重为它俩差的绝对值，转化为有权有向图最短路径问题，Dijkstra算法，O(M N lg(MN))。差的绝对值有个固定范围[1, 10 * 6]，而且对范围内每个数能以O(MN)时间通过DFS/BFS判断它是否可作为备选至少有一条路从左上到右下，如果该数满足则范围为它右边，否则左边=>二分，O(MNlg(106))。

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        M, N = len(heights), len(heights[0])
        dirs = [(-1, 0), (1, 0), (0, 1), (0, -1)]
        def bfs(limit):
            visited, q = {(0, 0)}, deque([(0, 0)])
            while q:
                r, c = q.popleft()
                if (r, c) == (len(heights) - 1, len(heights[0]) - 1): return True
                for (dx, dy) in dirs:
                    x, y = r + dx, c + dy
                    if len(heights) > x >= 0 <= y < len(heights[0]) and abs(heights[r][c] - heights[x][y]) <= limit and (x, y) not in visited:
                        q.append((x, y))
                        visited.add((x, y))
            return False
        s, e = 0, 10 ** 6
        while s < e:
            m = s + e >> 1
            if not bfs(m):
                s = m + 1
            else:
                e = m 
        return s