1235. Maximum Profit in Job Scheduling

https://leetcode.com/problems/maximum-profit-in-job-scheduling/

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

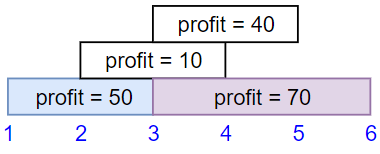
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

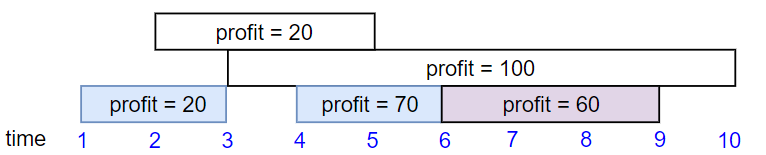
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4

• 1 <= startTime[i] < endTime[i] <= 10^9

• 1 <= profit[i] <= 10^4

给定一系列任务，每项任务有<初始时间，终止时间，利润>，同一时间只能执行一项任务，问最大利润能有多少。此题表面是区间问题，但如果陷入区间问题的思路（如扫描线，区间合并等）就掉入了陷阱。本质上是个选子集的问题，每个job有选or不选=>DP。时间可以看作是一种特殊的背包，dp是一个treemap，dp[i]表示截止到时间点i，最大的利润是多少。根据任务的endTime作排序并遍历。针对选当前任务i时，利用tree map快速定位到截止到startTime时最大利润是多少并加上当前任务的profit，与不选i时最大利润比较，如果大则把i插入dp。

/*
 * @lc app=leetcode id=1235 lang=cpp
 *
 * [1235] Maximum Profit in Job Scheduling
 */

// @lc code=start
class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        const int N = startTime.size();
        vector<vector<int>> jobs(N, vector<int>(3));
        for (int i = 0; i < N; ++i) {
            jobs[i][0] = endTime[i];
            jobs[i][1] = startTime[i];
            jobs[i][2] = profit[i];
        }
        sort(jobs.begin(), jobs.end());
        map<int, int> dp = {{0, 0}};
        for (const auto &job : jobs) {
            const auto cur = prev(dp.upper_bound(job[1]))->second + job[2];
            if (cur > dp.rbegin()->second) dp[job[0]] = cur;
        } 
        return dp.rbegin()->second;
    }
};
// @lc code=end