1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance

https://leetcode.com/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

Example 1:

Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2] 
City 1 -> [City 0, City 2, City 3] 
City 2 -> [City 0, City 1, City 3] 
City 3 -> [City 1, City 2] 
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1] 
City 1 -> [City 0, City 4] 
City 2 -> [City 3, City 4] 
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3] 
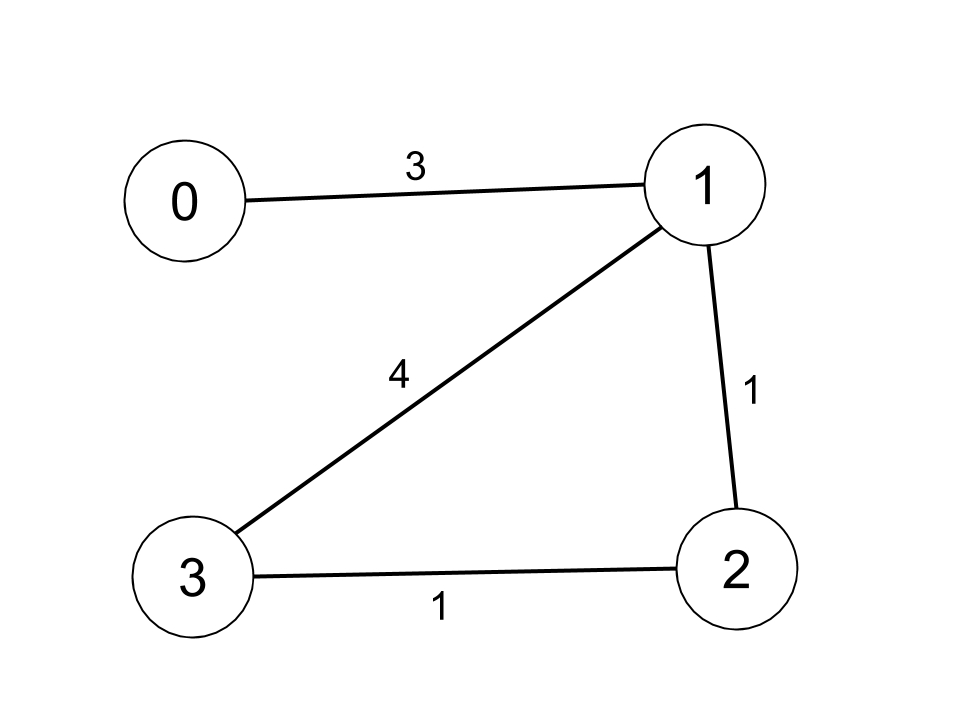
The city 0 has 1 neighboring city at a distanceThreshold = 2.

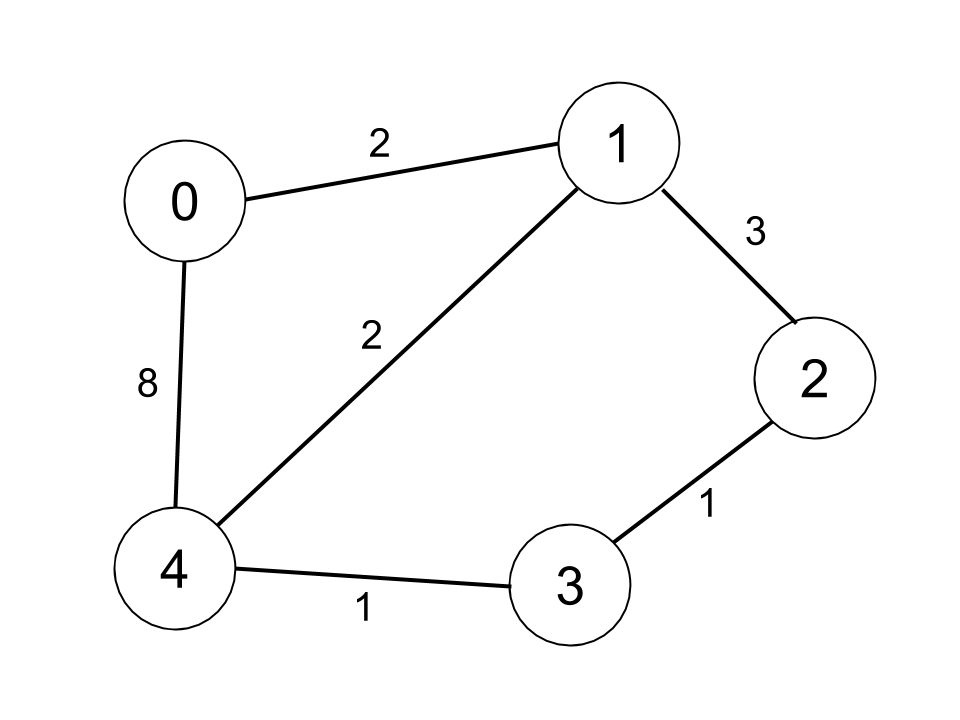
Constraints:

• 2 <= n <= 100

• 1 <= edges.length <= n * (n - 1) / 2

• edges[i].length == 3

• 0 <= fromi < toi < n

• 1 <= weighti, distanceThreshold <= 10^4

• All pairs (fromi, toi) are distinct.

有权无向图上每个结点最远能走阈值所设定的距离，找能访问到结点数最少的结点。找图上所有结点对的距离，然后再做筛选并找出拥有reachable最少的结点。找所有结点对距离用Floyd算法，基于DP思想：dp[i][j]存[i,j]最短距离，遍历所有节点k并把该节点k看作中转节点，看dp[i][k] + dp[j][k]是否比当前dp[i][j]更小，是就更新。

class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<int>> dp(n, vector<int>(n, INT_MAX / 2));
        for (int i = 0; i < n; ++i) dp[i][i] = 0;
        for (const auto &e : edges) {
            dp[e[0]][e[1]] = e[2];
            dp[e[1]][e[0]] = e[2];
        }
        for (int k = 0; k < n; ++k) {
            for (int i = 0; i < n; ++i) {
                for (int j = 0; j < n; ++j) {
                    if (dp[i][j] > dp[i][k] + dp[k][j]) dp[i][j] = dp[i][k] + dp[k][j];
                }
            }
        }
        auto m = INT_MAX, res = -1;
        for (int i = n - 1; i >= 0; --i) {
            auto cnt = 0;
            for (int j = 0; j < n; ++j) {
                if (i == j) continue;
                if (dp[i][j] <= distanceThreshold) ++cnt;
            }
            if (cnt < m) {
                m = cnt;
                res = i;
            }
        }
        return res;
    }
};